iBPE: 초고속 정규표현식 말뭉치 검색 알고리즘
한국어 역사 말뭉치 검색 플랫폼인 'ᄎᆞ자쎠'를 사용하다 보면, 정규표현식(RegEx)으로 검색하는 것이 유용한 때가 있다.
한 예를 들자면, 'ᄎᆞᆽ다'의 활용형 'ᄎᆞᄌᆞ니'와 이형태 'ᄎᆞ즈니'를 포함하여 한 번에 검색하려면 /cho\.c[ou]\.ni/와 같이 검색할 수 있다.
그러나 기존의 풀텍스트 검색(full-text search) 알고리즘으로는 이러한 정규 표현식 검색을 빠르게 수행할 수 없다. 말뭉치 검색이 느린 것은 큰 문제이다. 검색 결과를 기다리는 동안 새로운 검색어를 시도해 볼 기회가 뺏기는 것이기 때문이다.
이 글에서는 내가 이 문제를 해결하기 위해 새롭게 만든 iBPE 색인(inverse Byte-Pair Encoding Indexing)을 소개한다. iBPE를 소개하기에 앞서 이해의 도움을 위해 기존의 풀텍스트 검색 가속을 위한 여러 알고리즘을 설명하도록 하겠다.
순차적 접근 방법
말뭉치를 검색하는 가장 단순한 방법으로는 순차적 접근(sequential scan)이 있다. 이 방법은 말 그대로, 말뭉치의 모든 문장을 하나하나 보면서 주어진 검색어와 일치하는 부분이 있는지 보는 것이다. 예를 들어 아래와 같이 다섯 문장으로 구성된 단순한 말뭉치를 고려해 보자 (각 문장 앞의 숫자는 문장에 부여된 고유 ID(식별자)이다.)
1: "빌려 온 고양이 같다."
2: "말 달리자!"
3: "고양이 목에 방울 달기다."
4: "빛 좋은 개살구"
5: "고양이한테 생선을 맡겼다."
순차적 접근은 다음과 같다. "고양이"라는 검색어가 주어지면, 1번부터 5번 문장까지 순차적으로 보면서, 각 문장에 "고양이"라는 단어가 포함돼 있는지 검사한다. 즉, 1번 문장에 "고양이"가 있는지 검사한다. 있다면, '1'을 리스트에 추가한다. 다음, 2번 문장에 "고양이"가 있는지 검사한다. 없으니, 다음 문장으로 넘어간다. 이와 같은 과정을 모든 문장을 볼 때까지 반복한다.
이 방법은 단순하지만 말뭉치에 문장의 수가 많다면 그 문장의 수에 비례하여 검색이 느려진다. 즉 말뭉치에 100만 문장이 있다면, 문장이 10개 있을 때보다 검색을 하는 데 10만 배 더 많은 시간이 걸릴 것이다. 즉, 순차적 접근 방법은 말뭉치의 크기가 클수록 사용하기 곤란해진다. 'ᄎᆞ자쎠'에는 2025년 현재 1백70만여 개의 문장이 등록되어 있다. 따라서 검색 요청이 들어올 때마다 순차적 접근을 사용하여 문장을 검색하면 매우 느릴 것이다.
색인 (indexing)
위의 순차적 접근 방법의 속도 문제를 해결하기 위해 색인(indexing)이라는 방법이 고안되었다. 사실 색인이라는 것은 디지털 시대 이전부터 존재하던 고전적인 검색 방법이다. 여느 두꺼운 책 뒷부분을 펼쳐 보면 아래 그림같이 생긴 색인(index)이 포함돼 있다.

색인은 책에서 사용된 중요 키워드들을 모아, 가나다 (혹은 알파벳) 순으로 배열하고 각 키워드가 책의 몇 페이지에 쓰여 있는지를 나타낸 것이다. 이러한 색인이 미리 만들어져 있으면 예컨대 책에서 "가변 초점 렌즈" 라는 단어를 찾기 위해 1페이지부터 890페이지까치 하나하나 넘겨보면서 찾을 필요가 없어진다. 대신 가나다순으로 배열된 색인에서 해당 단어를 찾은 뒤, 연결된 페이지 번호로 책을 넘기기만 하면 그만이다.
이렇게 구성된 색인을 다른 말로 역(逆)색인(inverted index)라고도 한다. 원본 텍스트에서는 순차적으로 정렬되어 있는 각 페이지 번호가 단어의 목록에 대응되는데 (책에서 특정 페이지를 찾으면 대응되는 단어들이 나열돼 있는 것을 떠올려 보라), 역으로 색인 파트에서는 순차적으로 정렬되어 있는 각 단어가 페이지 목록에 대응되는 것에서 이런 이름이 붙은 것이다.
이 아이디어를 말뭉치에 똑같이 적용할 수 있다. 즉 미리 말뭉치에 있는 각 어절을 모두 모아 "어절 -> 문장 번호 목록" 형식의 데이터를 가나다 순으로 정렬해 놓는 것이다. 이것을 아까의 예시에 적용하면 아래와 같은 색인을 만들 수 있다.
== ㄱ ==
같다 -> 1
개살구 -> 4
고양이 -> 1, 3
고양이한테 -> 5
== ㄷ ==
달기다 -> 3
달리자 -> 2
== ㅁ ==
말 -> 2
... (이하 생략)
이 색인은 만드는 시간이 오래 걸리고 저장 공간을 추가로 차지한다는 단점이 있지만, 한번 만들어 놓고 나서는 검색이 매우 빨라진다는 이점이 있다. 위 색인을 활용하여 "고양이"라는 어절이 어느어느 문장에 들어 있는지를 검색하려면, 가나다순의 색인에서 '고양이'를 찾은 다음, 화살표를 따라가면 "1, 3"번 문장이라는 것을 쉽게 알 수 있다.
세계 최대 영어 말뭉치 검색 사이트인 www.english-corpora.org에서 바로 이 어절 단위 색인을 사용하여 검색을 수행한다.
그러나 이 방법에는 치명적인 단점이 존재한다. 이렇게 어절 단위로 만든 색인으로는 어절과 정확히 맞지 않는 단위로는 검색을 할 수 없다는 점이다. 예컨대, 이 색인을 사용하여 "양이 같"이라는 문자열이 들어 있는 문장을 쉽게 검색할 수 없다 (단순 순차 접근으로는 가능하다). 그러나 이러한 부분적인 어절이 포함된 문장을 찾는 것은 말뭉치 검색에서 매우 흔히 요구되는 사항이다.
영어는 고립어(isolating language)의 특성이 강하기 때문에 어절 단위의 검색으로도 충분히 아쉽지 않다. "run" 같은 동사도 기껏해야 "run", "ran", "runs" 세 개 정도의 활용형이 있을 뿐이다. 그러나 한국어와 같이 체언과 용언의 형태 변화가 다채로운 언어에서는 어절 단위의 검색만으로는 충분하지 않다. 예컨대 "ᄎᆞᆽ다"의 모든 활용형들을 검색하려면, "ᄎᆞᆺ고, ᄎᆞᆺᄂᆞᆫ, ᄎᆞ자, ᄎᆞᄌᆞ니, ᄎᆞᄌᆞ며, ᄎᆞᄌᆞ시니라, ᄎᆞᄌᆞ샤ᄉᆞᅌᅵ다, …" 등등의 셀 수 없이 많은 활용형들을 모두 일일이 찾아볼 수는 없기 때문이다.
이 단점을 극복하려면 어떻게 해야 할까?
n-gram 색인 (n-gram indexing)
위의 문제점을 극복하기 위해 n-gram indexing 이라는 방법이 고안되었다. 우선, 말뭉치의 모든 문장을 자소 단위로 쪼갠다 ('ᄎᆞ자쎠'에서는 아래와 같이 한글을 로마자로 변환한다).
1: pil.lye Gwon kwo.GyaG.Gi kath.ta
2: mal tal.li.ca
3: kwo.GyaG.Gi mwok.Gey paG.Gwul tal.ki.ta
4: pich cwoh.Gun kay.sal.kwu
5: kwo.GyaG.Gi.han.they sayG.sen.Gul math.kyess.ta
그 다음, 문장에 들어 있는 모든 연속된 n 자소(n-gram)들을 추출한다. 보통 n=3 을 사용한다.
1: 'pil', 'il.', 'l.l', '.ly', 'lye', 'ye ', 'e G', ..., '.ta'
2: 'mal', 'al ', 'l t', ' ta', 'tal', 'al.', 'l.l', ..., '.ca'
...
5: 'kwo', 'wo.', 'o.G', '.Gy', 'Gya', 'yaG', 'aG.', ..., '.ta'
그 다음, 어절 대신 이 n-gram들을 사용하여 색인을 만들면 n-gram 색인이 완성된다. 즉, 각 n-gram에 대해 그 n-gram이 등장하는 문장 번호들의 집합을 연결짓는다.
'aG.' -> {1, 3, 5}
'al ' -> {2}
'al.' -> {2, 3, 4}
'an.' -> {5}
'ath' -> {1, 5}
'ay.' -> {4}
'ayG' -> {5}
... (이하 생략)
이렇게 어절 단위의 색인 대신 n-gram 색인을 만들면, "양이 같"과 같은 부분적인 문자열도 비교적 손쉽게 검색할 수 있다. 그 방법은 다음과 같다.
우선 검색할 문자열을 동일한 방식으로 자소 단위로 쪼갠다.
"양이 같" -> "GyaG.Gi kath"
그 다음, 여기서 n-gram들을 추출한다.
"GyaG.Gi kath" -> 'Gya', 'yaG', 'aG.', 'G.G', ..., 'ath'
추출된 각 n-gram에 대하여 색인을 찾아 등장하는 문장 번호들을 알아낸다.
'Gya' -> {1, 3, 5}
'yaG' -> {1, 3, 5}
...
'Gi ' -> {1, 3}
'i k' -> {1}
...
'ath' -> {1, 5}
그 다음, 찾아낸 문장 번호들의 집합의 교집합(∩)을 구한다.
{1, 3, 5} ∩ {1, 3, 5} ∩ {1, 3} ∩ {1} ∩ {1, 5} = {1}.
즉, "양이 같"이라는 문자열은 말뭉치 전체에서 1번 문장 외에는 등장할 수 없다는 사실을 알아냈다. 여기서 주의할 점은, 찾아낸 문장 번호 집합에 실제로는 검색어가 등장하지 않는 문장도 포함돼 있을 수 있다는 점이다. 따라서, 마지막 단계로서 찾은 문장 번호 집합 안에서 순차적 접근을 통해 최종 결과를 가려내야 한다. 그렇지만 위 방법으로 이미 대다수의 일치하지 않는 문장을 제외했기 때문에 이 순차적 접근이 많은 시간을 소요하지는 않는다. 또, 반대로 검색어가 등장하는 문장은 교집합에 반드시 포함되어 있음이 보장되기 때문에 원하는 문장이 뽑히지 않을 걱정은 하지 않아도 된다.
이러한 n-gram 색인을 통한 검색 방법은 인기 있는 데이터베이스 관리 프로그램 PostgreSQL의 한 기능으로 포함되어 있으므로 누구나 쉽게 사용할 수 있다.
n-gram 색인을 통한 정규 표현식 검색과 문제점
n-gram 색인을 통해 단순한 문자열 검색은 가속할 수 있는데, 정규 표현식 검색도 가속할 수 있을까?
결론부터 말하자면 일정 부분 가능하다. 그 방법은 전직 구글 엔지니어 Russ Cox의 블로그 글 "Regular Expression Matching with a Trigram Index"에 담겨 있다. 관심이 있다면 일독을 강력 추천한다. Russ Cox는 구글에서 Google Code Search(현재는 없어짐)에 정규표현식 검색을 지원하기 위해 이 알고리즘을 만들었다고 한다.
Cox의 알고리즘의 핵심 아이디어는, 주어진 정규표현식이 매치 가능한 (거의) 모든 문자열들의 n-gram들을 추출하여 집합 연산을 통해 최종 후보들을 얻어 오는 것이다.
예를 들어, /cho\.c[ou]\.ni/가 매치 가능한 문자열은 cho.co.ni와 cho.cu.ni 두 개가 있고, 첫 번째 후보에서는 'cho', 'ho.', 'o.c', '.co', 'co.', 'o.n', '.ni'들을 추출할 수 있으며, 두 번쨰 후보에서는 'cho', 'ho.', 'o.c', '.cu', 'cu.', 'u.n', '.ni'을 추출할 수 있다. 여기서 색인을 찾아 각 후보에 대해 문장 번호들의 교집합을 구한 뒤, 정답은 그 두 집합 둘 안에 포함돼 있으므로, 그 두 집합의 합집합을 구하여 최종 후보 집합을 만든다. 더 복잡한 정규 표현식에 대해서는 더욱 복잡한 집합 연산들을 해야 하게 된다.
이 방법으로 많은 정규 표현식에 대해 검색 속도를 향상시킬 수 있지만, 예컨대 /n[a-z]+m[a-z]+p[a-z]+/와 같이 경우의 수가 매우 많은 정규 표현식에 대해서는 정규 표현식이 매치할 수 있는 모든 경우의 수를 보느라 오히려 순차적 접근보다도 속도가 느려지게 된다.
n-gram 색인의 또다른 단점은 서로 다른 n-gram 간에 빈도수 불균형이 매우 심하다는 점이다.1
예를 들어, 영어 말뭉치에서 'the' 같은 n-gram은 'vzq' 같은 n-gram 보다 빈도수가 월등히 많을 것이다 (후자는 아예 존재하지 않을 수도 있다).
이것은 n-gram 색인을 통한 검색의 속도를 저해하는 요인이 된다. 검색어가 'to be or not to be'와 같이 빈도수가 매우 높은 단어들의 연속이라면, 전체 검색어가 흔하지 않더라도 검색어를 구성하는 각 n-gram들의 빈도수가 매우 높아 문장 후보들을 충분히 제외하지 못할 수도 있기 때문이다.
'ᄎᆞ자쎠'에서도 한동안 이 n-gram 색인을 통해 일반 검색과 정규 표현식 검색을 지원하였지만, 위와 같은 문제 때문에 성능이 벽에 부딪치게 되었다. 따라서 더 다양한 정규표현식을 지원하고 n-gram 빈도수의 불균형 문제를 해결할 수 있는 새로운 검색 방법의 필요성이 대두되었다.
iBPE 색인
BPE 토크나이저(Byte-Pair Encoding Tokenizer)는 GPT-2부터 사용되기 시작하여 요즘 LLM(대형언어모델)에서 입력과 출력 텍스트를 토큰(token)단위로 쪼개기 위해 가장 많이 사용되는 방법이다. 이 맥락에서 '토큰'이란 텍스트를 쪼개는 단위로, 자소보다는 크고 단어(word)보다는 클 수도, 작을 수도 있다.
BPE 토크나이저의 자세한 원리는 논외로 하나, BPE의 가장 중요한 성질은 각 토큰의 빈도수가 대체로 균일하게 되도록 토큰들의 집합이 구성되는 것이다. 이 성질로 인해 예컨대 'antidisestablishmentarianism'과 같은 빈도수가 낮은 어절은 'anti / dise / stablish / menta / rian / ism'과 같은 식으로 여러 토큰으로 쪼개지게 되고 (토큰이 형태소와 항상 일치하지는 않음), 'of the'와 같이 빈도수가 높은 어절의 연속은 하나의 토큰으로 합쳐지게 된다.
토큰의 수는 미리 정하는데, 보통 1000개에서 10만 개 사이가 흔히 사용된다. 만약 4096개의 토큰을 사용한다면, 각 토큰에 1부터 4096까지의 토큰 번호가 부여된다.
즉 여섯 개의 토큰으로 쪼개진 'anti / dise / stablish / menta / rian / ism'이 예컨대 1423 27 232 40 39 4039 2077과 같이 대응되는 6개의 숫자로 저장되는 것이다.
이렇게 텍스트를 토큰으로 쪼개고 각 토큰에 대응하는 숫자로 변환하는 것을 '토큰화'(tokenization)라고 한다.
만약 우리의 말뭉치 속의 모든 문장을 이렇게 BPE 토크나이저를 사용하여 토큰화한다면, 아까 어절 단위의 색인을 구성했던 것처럼, 각 BPE 토큰에 대해 해당 토큰이 등장하는 문장 번호의 집합을 대응시키는 색인을 구성할 수 있다. 이렇게 BPE로 색인을 구성한다면, 각 토큰의 빈도수가 비교적 균일해지므로 검색 효율이 올라갈 것을 기대할 수 있게 된다. 이렇게 BPE 토크나이저를 사용해 구성한 색인을 iBPE 라고 이름 붙였다.
그런데 실제로 이렇게 구성된 iBPE 색인을 사용하여 문자열을 검색하는 것은 단순하지는 않다. BPE의 특성 상 한 문자열이 토큰화되는 방법은 유일하지 않고, 같은 문자열이 여러 다른 토큰열로 토큰화될 수 있기 때문이다. 예컨대, 위의 단어는 'ant / idis / estab / lishme / ntar / ianism'과 같이 토큰화될 수도 있다 (만약 이러한 토큰들이 모두 토큰 집합에 존재한다면). 정규표현식 검색도 따라서 더 복잡해지게 된다.
iBPE 검색 알고리즘
iBPE 검색 알고리즘을 설명하려면, 먼저 정규표현식의 기본적인 성질에 대해 알아볼 필요가 있다.
모든 정규표현식은 유한상태기계(FSM: Finite State Machine)로 변환될 수 있다.2
변환하는 알고리즘은 여러 가지가 있지만, McNaughton-Yamada-Thompson 알고리즘이 대표적이다.
예컨대, /n[a-z]+m[a-z]+p[a-z]+/라는 정규표현식을 DFA(Deterministic Finite Automaton)로 변환한다면 다음과 같은 그림이 된다.
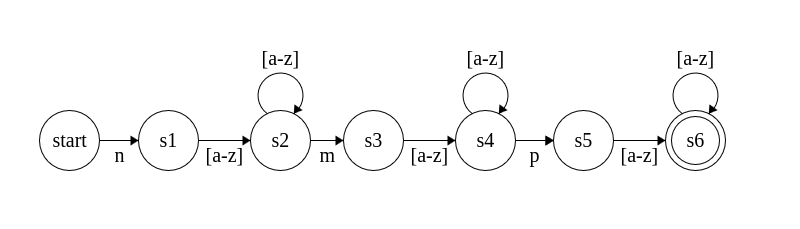
이제 앞으로 사용될 표기법을 정의하도록 한다. 주어진 정규표현식을 DFA로 변환한 것을 \(M\)이라고 하자.
\(\mathcal{I}(t)\)는 iBPE 색인을 참조하는 함수이다.
\[\mathcal{I}(t) := \{(\sigma, i, i+1)\ |\ \text{토큰 $t$가 토큰화된 문장 $\sigma$의 $i$번째 위치에 있음}\}.\]A와 B가 각각 \((\sigma, i, j)\) (\(\sigma\)는 문장 번호, i, j는 문장 내 토큰 위치를 나타냄) 튜플들로 구성된 집합들일 때, A에 소속된 토큰 범위가 B에 소속된 토큰 범위로 곧장 이어지는 범위들의 집합 \((A \Rightarrow B)\)는 다음과 같이 정의한다.
\[(A \Rightarrow B) := \{ (\sigma, i, j)\ |\ (\sigma, i, k)\in A\ \land\ (\sigma, k, j) \in B \}.\]또, 상태 \(s\)에서 출발하여 기각(reject) 없이 소모(consume) 가능한 토큰들의 집합을 다음과 같이 나타내자.
\[G(s) := \{ (t, s_{new})\ |\ \text{$M$이 상태 $s$에서 $t$번째 토큰에 대응하는 문자열을 소모하면 상태 $s_{new}$로 전이함} \}.\]마지막으로, 상태 s에서부터 채택 가능한 문장 번호(와 토큰 위치)들의 집합을 다음과 같이 나타내자.
\[\begin{aligned} D(s) := \{(\sigma, i, j)\ |&\ \text{$M$이 상태 $s$에서 문장 $\sigma$의 i번째 위치에서 j번째 위치까지의} \\ &\text{ 토큰들을 소모했을 때 채택(accept) 상태가 됨}\}. \end{aligned}\]이 \(D(s)\)는 재귀적으로 다음과 같이 계산할 수 있다.
\[\begin{align} D(s) &= \bigcup_{(t, s_{new}) \in G(s)} \left(\mathcal{I}(t) \Rightarrow D(s_{new})\right), \\ D(s_{accept}) &= U. \end{align}\]따라서, 우리가 원하는 문장 번호들의 집합 \(D(s_{start})\)는 위 식을 동적 프로그래밍(Dynamic programming)으로 계산하면 얻을 수 있다.
구현
iBPE 색인 검색 알고리즘을 PostgreSQL 확장 기능으로 구현하였다. Github에서 찾을 수 있다.
성능
다음은 PostgreSQL에 구축한 'ᄎᆞ자쎠'의 말뭉치 DB를 검색하는 데 걸리는 시간(latency)을 나타낸 것이다.3
| Keyword | ho |
si.ta.so.ngi.ta |
/cho\.c[ou]\.ni/ |
/[一-鿌㐀-䶵]`i/ |
|---|---|---|---|---|
| Seq. scan | 648ms | 1128ms | 1116ms | 709ms |
| Seq. scan (par.) | 659ms | 418ms | 373ms | 242ms |
| n-gram index | 251ms | 194ms | - | - |
| iBPE index | 244ms | 23.8ms | 20.0ms | 277ms |
iBPE 검색은 단순 문자열과 정규표현식 검색에서 뛰어난 검색 속도를 보여준다.
현재 'ᄎᆞ자쎠'에 iBPE 검색이 적용되어 있다. 사용해 보자!