고양이는 왜 털이 무한정 자라지 않을까?
인간은 정기적으로 미용실에 가서 머리카락을 자른다. 자르지 않으면 아래 그림의 라푼젤과 같이 무한정 길어질 것이기 때문이다.

반면, 오른쪽에 있는 고양이는 몸통이 무한정 늘어날망정, 온몸을 뒤덮고 있는 털은 무한정 길어지지 않는다. 고양이는 우리가 모르는 사이에 정기적으로 고양이 미용실에라도 갔다 오는 것일까? 그런 게 아니라면 어떻게 해서 고양이의 털은 무한정 길어지지 않고 일정 수준을 유지할 수 있는 것일까? 고양이 몸을 뒤덮고 있는 각각의 털이 자신이 얼마나 긴지를 알고 있다가 일정 길이 이상 늘어나면 모낭에게 더 이상 자라지 말라는 신호라도 보내는 것일까? 그러나 털은 신경이 없기 때문에 자신이 얼마나 긴지를 아는 건 불가능하다.
당신이 고양이 집사라면 아마 이 물음에 대해 아래와 같은 해답을 생각할 것이다.
아니, 고양이는 하루에도 수십 번 혀로 몸 구석구석 그루밍을 하잖아?
그건 사실이다. 하지만 조금만 생각해 봐도 이게 완전한 해답은 아니라는 것을 알 수 있다.
고양이는 혀로 몸을 골고루 핥고, 이로 인해 매번 상당수의 털이 빠져나온다. 그러나 이것은 인간이 미용실에 가서 커트를 받는 것과 결코 같은 효과가 될 수 없다. 왜냐하면 미용사는 일정 길이 이상의 머리카락만을 선별하여 자름으로써 머리카락의 최대 길이가 특정 길이 이하가 되도록 보장할 수 있지만, 고양이의 혀는 털의 길이를 선별할 수 있는 능력이 없기 때문이다.
그럼 도대체 고양이의 털 길이는 어떻게 일정 수준으로 유지될 수 있는 것일까?
이 문제에 대한 답을 얻어내기 위해서 아래와 같은 확률 모델을 생각해 보자.
\[\begin{align} {\boldsymbol l}_0 &= 0, \\ {\boldsymbol l}_{i + 1} &= \begin{cases} {\boldsymbol l}_{i} + r & \text{w.p. } 1 - p \\ 0 & \text{w.p. } p \end{cases}. \end{align}\]즉, 처음에는 털의 길이가 0이고, 1초가 지날 때마다 \(p\)의 확률로 털이 빠져 길이가 0으로 리셋되거나, 빠지지 않는다면 \(r\) 만큼 털이 자란다. 이 모델의 특성은 털이 빠지느냐, 빠지지 않느냐는 털의 길이와 관련없이 시간당 일정한 확률이 적용된다는 것이다. (이것을 Markov Property라고도 한다.) 이 모델에서 털의 길이의 기댓값은 수렴할까, 발산할까?
나는 우선 \(p=0.1\%, r=1\)으로 놓고 시뮬레이션을 1000번 돌려보았다. 털의 길이의 기댓값은 시간이 지날수록 특정 값으로 수렴하는 것을 볼 수 있다.
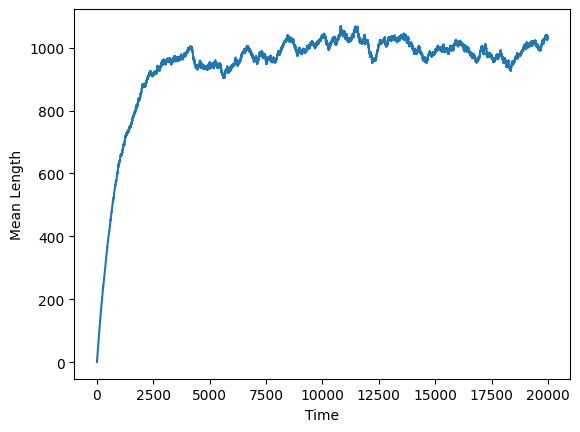
그렇다면 정확히 어떤 값에 수렴할까? 그건 \(\lim_{i \rightarrow \infty} \mathbb{E}\left[ {\boldsymbol l}_{i} \right]\)의 극한을 계산해 보면 알 수 있다.
\[\begin{align} l_{\infty} &:= \lim_{i \rightarrow \infty} \mathbb{E}\left[ {\boldsymbol l}_{i} \right] \\ &= (1 - p) \cdot (l_{\infty} + r) + p \cdot 0. \\ \implies l_{\infty} &= \frac{r(1 - p)}{p} \\ &= \frac{1(1 - 0.001)}{0.001} = 999. \end{align}\]즉, 매 초마다 1mm씩 자라는데, 매 초마다 빠질 확률이 0.1%인 털의 길이는 평균적으로 999mm의 길이에 수렴한다.
털이 빠지는 일이 그 털의 길이와 관련이 없어도, 평균적인 털의 길이는 털이 빠질 확률과 털이 자라는 속도 두 변수만으로 결정되는 일정한 길이에 수렴한다는 사실을 알 수 있다. 고양이 털의 미스터리가 해결된 것일까?
그런데 고양이는 털이 하나만 있는 것이 아니라 굉장히 많이 있다. 그 모든 털들의 길이의 평균값이 무한정 늘어나지 않는다고 해도, 그 중에서 가장 긴 털이 무한정 늘어나지 않는다는 보장이 있을까? 사실 조금만 생각해 보아도, 어떤 집단의 평균값이 유한하다면, 그 집단의 최댓값도 유한할 것이라는 결론은 쉽게 내릴 수 있다. 왜냐하면, 집단에서 하나의 값만 무한대라고 하더라도, 전체의 평균값은 무한대가 되어 버리기 때문이다.
그러나 그래도 가장 긴 털의 길이는 평균 털의 길이보다 얼마나 더 길지가 궁금하다. 또, 내가 아는 고양이의 털 개수와 평균 털 길이를 알고 있으면, 그 고양이의 털이 자라는 속도와 털이 빠지는 확률도 알 수 있을까? 그 답을 하기 위해서는 우리의 모델을 좀더 개선할 필요가 있다.
우선, 실세계의 고양이의 털은 초침이 움직일 때마다 얼마씩 이산적으로 자라지 않고, 연속적으로 자란다. 또, 털이 떨어지는 것도 이산적으로 이루어지는 게 아니다. 이 연속성을 생각하기 위해 털 길이의 모델을 아래와 같이 수정하자.
\[\begin{align} {\boldsymbol l}_0 &= 0, \\ {\boldsymbol l}_{i + \epsilon} &= \begin{cases} {\boldsymbol l}_{i} + \epsilon r & \text{w.p. } 1 - \epsilon p \\ 0 & \text{w.p. } \epsilon p \end{cases}. \end{align}\]\(\epsilon\) 이라는 변수를 도입하여 1초마다 털이 자라는 것 대신, 매 \(\epsilon\)초마다 털이 자라고 빠지는 것으로 바꾸었다. 이제 이 모델에서 \(\epsilon\)을 무한소로 보내면 연속적으로 자라는 털의 모델이 될 것이다. \({\boldsymbol l}_1, {\boldsymbol l}_2, {\boldsymbol l}_3, \dots\)의 확률 분포를 확인해 보자. \(\alpha := 1 - \epsilon p, \beta := \epsilon p\)으로 놓았다.
\[\begin{align} {\boldsymbol l}_{1\epsilon} &= \begin{cases} 0 & \text{w.p. } \beta \\ \epsilon r & \text{w.p. } \alpha, \\ \end{cases} \\ {\boldsymbol l}_{2\epsilon} &= \begin{cases} 0 & \text{w.p. } \beta \\ \epsilon r & \text{w.p. } \alpha \beta \\ \epsilon 2r & \text{w.p. } \alpha^2, \\ \end{cases} \\ {\boldsymbol l}_{3\epsilon} &= \begin{cases} 0 & \text{w.p. } \beta \\ \epsilon r & \text{w.p. } \alpha \beta. \\ 2\epsilon r & \text{w.p. } \alpha^2 \beta. \\ 3\epsilon r & \text{w.p. } \alpha^3. \\ \end{cases} \\ \end{align}\]이제 패턴이 보일 것이다. 즉 \(n\)번 반복 후의 털 길이는,
\[\begin{align} {\boldsymbol l}_{n\epsilon} &= \begin{cases} 0 & \text{w.p. } \beta \\ \epsilon r & \text{w.p. } \alpha \beta. \\ 2\epsilon r & \text{w.p. } \alpha^2 \beta. \\ \vdots \\ (n-1)\epsilon r & \text{w.p. } \alpha^{n-1} \beta. \\ n\epsilon r & \text{w.p. } \alpha^n. \\ \end{cases} \\ \end{align}\]위와 같은 확률 분포를 가지게 된다. \(t = n\epsilon\)으로 놓고 \(\epsilon\)이 무한히 작아질 때 \({\boldsymbol l}_{t}\)의 누적확률분포함수(cdf)를 구해보면,
\[\begin{align} F_{l_t}(l) &= Pr({\boldsymbol l}_{t} \leq l) \\ &= \beta \cdot (1 + \alpha + \alpha^2 + \dots + \alpha^{l/{\epsilon r}}) \\ &= 1 - \exp\left(-\frac{p l}{r}\right) \end{align}\]이 된다. 따라서 털이 N개(i.i.d.)일 경우 그 최댓값의 누적확률분포함수는 다음과 같다.
\[\begin{align} F_N(l) &= Pr({\boldsymbol l}_{t}^{(1)} \leq l \land \dots \land {\boldsymbol l}_{t}^{(N)} \leq l) \\ &= Pr({\boldsymbol l}_{t}^{(1)} \leq l) \cdot \dots \cdot Pr({\boldsymbol l}_{t}^{(N)} \leq l) \\ &= F_{l_t}(l)^N \\ &= \left(1 - \exp\left(-\frac{p l}{r}\right)\right)^N. \end{align}\]이 결과를 미분해서 확률밀도함수(pdf)를 구해서 기댓값을 구할 수 있다.
\[\begin{align} f_N(l) &= F'_N(l) \\ &= \frac{Np}{r} \left(1-\exp\left(-\frac{pl}{r}\right)\right)^{N-1} \exp\left(-\frac{pl}{r}\right). \end{align}\] \[\begin{align} \mathbb{E}[\max \{ {\boldsymbol l}_{t}^{(1)}, \dots, {\boldsymbol l}_{t}^{(N)} \}] &= \int_0^\infty l f_N(l) \mathrm{d}l \\ &= \frac{r}{p} \cdot H_N. \end{align}\]여기서 \(H_N\)은 \(N\)번째 조화수이다. 여기서 \(N=1\)일 경우, \(H_1 = 1\)이므로, 즉 털이 한 가닥일 경우 털 길이의 기댓값은 \(\frac{r}{p}\)라는 걸 알 수 있다.
마지막으로 실제 값들을 한번 대입해 보자.
구글 검색에 따르면 일반적인 고양이는 1천 5백만 ~ 4천만 개의 털이 있다고 한다. 대충 2천만 (=\(2\times 10^7\)) 개라고 치자. 그리고 털이 자라는 속도는 1달에 1.5cm 정도, 즉 하루에 0.5mm 정도라고 한다. 만약 털 하나가 하루동안 빠질 확률이 5%라고 하면, 털 길이의 기댓값은 \(0.5 / 0.05 = 10mm\)에 수렴하고, 모든 털의 길이의 최댓값의 기댓값은 \(10 \cdot H_{2\times 10^7} = 174mm\)가 된다. 즉, 평균 털의 길이가 1cm인 고양이의 몸에는 잘 찾아보면 17.4cm에 육박하는 털이 하나쯤 있을 수도 있다는 뜻이다(!)